Chapter 1

 

Introduction to LTSpice

 

Gordon W. Roberts

Department of Electrical & Computer Engineering, McGill University

 

 

This chapter introduces electronic circuit simulation using Spice, and outlines the basic philosophy of circuit simulation and explains why it has become so important for today's electronic circuit design. We then summarize the capabilities of Spice and the computer conception of electrical and electronic elements and give examples. Spice is an acronym for Simulation Program with Integrated Circuit Emphasis. The Spice platform used to illustrate these concepts will be the freely available Spice program called LTSpice supplied by Analog Devices, Inc.  The prefix LT before the word Spice stands for Linear Technologies; the name of the company that created this program before being acquired by Analog Devices, Inc (ADI).

 

Throughout this document, various LTSpice examples are shown.  These were generated using LTSpice running on an OS X operating system.  For those operating on a Windows operating system, some displays will appear different.  However, the main thrust of what is described below is the same.

 

1.1 Computer Simulation of Electronic Circuits

 

Traditionally, electronic circuit design was verified by building prototypes, subjecting the circuit to various stimuli such as input signals, temperature changes, and power supply variations, then measuring its response using appropriate laboratory equipment. Prototype-building is somewhat time-consuming but produces practical experience from which to judge the manufacturability of the design.     

 

The design of an integrated circuit (IC) requires a different approach. Due to the minute dimensions associated with the IC, a breadboarded version of the intended circuit will bear little resemblance to its final form.  The parasitic components that are present in an IC are entirely different from the parasitic components present in the breadboard, and signal measurements obtained from the breadboard usually don't provide an accurate representation of the signals appearing on the IC. 

 

Measuring the appropriate signals directly on the IC itself requires extreme mechanical and electrical measurement precision and is limited to specific types of measurements (i.e., it is very difficult to measure currents). Furthermore, an IC implementation does not lend itself easily to circuit modifications which must be made at the IC mask level prior to circuit fabrication.  Due to processing delay time, this approach may result in weeks between executing the modification and observing its effect.

 

Computer programs that simulate the performance of an electronic circuit provide a simple, cost-effective means of confirming the intended operation prior to circuit construction and of verifying new ideas that could lead to improved circuit performance.  Such computer programs revolutionized the electronics industry, leading to the development of today's high-density monolithic circuit schemes such as VLSI.  Spice, the de-facto industrial standard for computer-aided circuit analysis, was developed in the early 1970s at the University of California, Berkeley. Although other programs for computer-aided circuit analysis exist and are being used by many different electronic design groups, Spice is the most wide-spread. Originally written for main-frame computers, today we find various versions of Spice for personal computers (PCs). In general, these programs use algorithms slightly different from Spice's for performing the circuit simulations, but many of them adhere to the same input format description, elevating the Spice input syntax to a computer-like language.

 

Commercially supported versions of Spice can be considered to be divided into two types: main-frame versions and PC-based versions. Generally, main-frame versions of Spice are intended to be used by sophisticated integrated-circuit designers who require large amounts of computer power to simulate complex circuits. Commercial versions of Spice include, but limited to, HSpice from Meta-Software now Synopsys and PSpice originally from the MicroSim Corporation and now distributed by Cadence Design Systems.

 

Although Spice was originally intended for analyzing integrated circuits, its underlying concepts are general and can apply to any type of network that can be described in terms of a basic set of electrical elements (i.e., resistors, capacitors, inductors, and dependent and independent sources). Today, Spice is often used for such applications as the analysis of high-voltage electrical networks, power management and feedback control systems, and the effect of thermal gradients on electronic networks.

 

Integrated circuit design usually begins with a set of specifications (e.g., frequency response, step-response, etc.). It is the designer's objective to configure an electronic circuit that satisfies these specifications. This task intrigues most circuit designers because so far computers have not yet acquired enough intelligence to do the design automatically, although great advances are being made every day with the advancement of machine learning and AI technologies. So, for now, the designer must rely on his or her knowledge of electronic circuit design. By using approximate methods of analysis, designs can be configured and quickly analyzed by hand to determine if they have the potential for meeting the proposed specifications.

 

Once a design is found that might meet the specifications, the designer applies more complex models of device behavior (such as those in Spice). The behavior of the design, as simulated by Spice, is checked against the required specifications. If the circuit fails to meet the specs, the designer can return to a simpler computer model, preferably the one used during the initial design, and identify the reason for the discrepancy. When computer simulation shows that the performance of a circuit is not adequate, the designer who understands the components of the design can systematically alter them to improve performance. (Otherwise, the designer must rely on a brute force hit-or-miss approach – one that usually results in a lot of wasted effort and probably no improvement to the circuit.) 

1.2 Types of Analysis Performed by LTSpice

 

LTSpice simulates the behavior of electronic circuits on a digital computer and tries to emulate both the signal generators and measurement equipment such as multimeters, oscilloscopes, curve-tracers and frequency spectrum analyzers. Here we briefly outline the analysis available in LTSpice and two different ways to describe a circuit to LTSpice. One input method is to write a sequence of lines using a text editor to create a computer file with suffix *.net and then direct LTSpice to read this file. The text file is commonly referred to as the Spice input file or netlist. As the input file contains analysis commands, when instructed, LTSpice will perform specific types of analysis. Another method is to capture a circuit schematic using the schematic entry tool of LTSpice, along with a set of analysis commands, which then creates a Spice input deck which can then be analyzed by LTSpice.  Below these two entry methods will be described. However, let us first describe the types of analysis that can be performed by LTSpice.  The following description is meant as only a brief introduction. Later chapters will provide more detailed examples.

 

LTSpice is a general-purpose circuit simulator capable of performing three main types of analysis---nonlinear DC, nonlinear transient, and linear small-signal AC circuit analysis.

 

Nonlinear DC analysis or simply DC analysis calculates the behavior of the circuit when a DC voltage or current is applied to it. In most cases, this analysis is performed first.  We commonly refer to the results of this analysis as the DC bias or operating-point characteristics.

 

The Transient Analysis, probably the most important analysis type, computes the voltages and currents in the circuit with respect to time. This analysis is most meaningful when time-varying input signals are applied to the circuit; otherwise this analysis generates results identical to the DC analysis.  The third is a small-signal AC analysis. It linearizes the circuit around the DC operating point, then calculates the network variables as function of frequency. This, of course, is equivalent to calculating the sinusoidal steady-state behavior of the circuit, assuming that the signals applied to the network have infinitesimally small amplitudes.

 

LTSpice is capable of performing other types of analysis which are generally viewed as special cases of the three main types.  We outline them below.

 

DC Sweep allows a series of DC operating points to be calculated while sweeping or incrementally changing the value of an independent current or voltage source. This analysis is used largely to determine the DC large-signal transfer characteristic. The Transfer Function analysis is related. It computes the small-signal DC gain from a specified input to a specified output (i.e., one of the following: voltage gain, transconductance, transresistance, or current gain), and the corresponding input and output resistance.

 

In manner similar to DC Sweep, Temperature Analysis allows a series of analyses to be performed while varying the temperature of the circuit. Because the characteristics of many devices depend on temperature, this facility provides a useful tool for investigating the effect of temperature variation on circuit operation. Any of the above main analysis types can be performed in conjunction with Temperature Analysis, thus providing insight into temperature dependencies.

 

Sensitivity Analysis indicates which components affect circuit performance most critically. (Critical components may require tighter manufacturing tolerances.) There are several ways in which to investigate the impact of component tolerances on a specific circuit behavior. One way is to perform a parameter sweep of a component value and observe the range of corresponding circuit behavior. Another is to assign a set of random numbers to different circuit components having either a Gaussian or uniform distribution and observe the overall statistical behavior of the circuit subject to various stimuli. The latter analysis is known as a Monte Carlo Analysis.

 

Finally, Noise and Fourier Analysis procedures calculate the dynamic range of a circuit.  Noise analysis calculates the noise contribution of each element, injects its effect back into the circuit and calculates its total effect on the output node in a mean-square sense. The Fourier analysis computes the Fourier series coefficients of the circuit's voltages or currents with respect to the period of the input excitation(s).

 

 

 

 

1.3. Preparing LTSpice for Analysis

 

There are two ways to describe a circuit to LTSpice; (1) text entry using the Spice Description Language (SDL), or (2) capture a schematic circuit using a specialized drawing tool. Both of these methods will be described in some detail below. The schematic capture tool generates as output an SDL text file. Regardless of the entry method, the resulting SDL file is passed to the simulation engine for a specific circuit analysis directive.  On execution, LTSpice creates four separate files in the user’s local directory.  Assuming the file was initially named myproject, the four files appear in the local directory as:

 

 

The file myproject.asc contains the details of the drawing objects used to construct the schematic circuit, along with component values and Spice analysis directives. The file is readable by a text editor. The second file myproject.net contains what is called the circuit netlist and is an SDL description of the drawn circuit. The format of this file has a very specific syntax that has become the defacto standard for all Spice-based tools across the electronics industry. The third file, myproject.raw, is a mixed text-binary data format file; at the top of the file is a text listing of the variables used in the simulation and their corresponding values.  The bottom part of the file is a binary data set corresponding to the waveforms requested by the SPICE directive. This data is read by LTSpice and is used to display the simulation results and any post-processing computational results in a graphical format. The fourth file, myproject.log, is a text file that lists the sequence of mathematical operations performed by LTSpice and some numbers related to the computational operations. The results of some analysis commands such as a Fourier and Noise analysis will appear in this file.  It is always a good idea to keep all four files open at the same time to see if any problems have occurred, as depicted in Fig. 1.1.   These files can be opened by placing one’s mouse in the myproject.asc window that first appears on one’s desktop on launching LTSpice. Click with the right-side mouse button, then selecting the View Tab in the pull-down menu that appears. Once enabled, a second level drop-down menu appears with a list of view options. This can be seen in the upper-left hand side of Fig. 1.1.  To open the log file, select the Spice Error Log tab that appears.  To open the netlist file, select the SPICE Netlist tab.  To display any waveform data, select the Waveform Data tab.  These four steps should be repeated for each and every simulation undertaken by the user.

As this may be the first time that you are using LTSpice, it is important to set the foreground and background colors of your windows.  This is done by clicking on the hammer icon  found in the upper left-hand side of any one of the opened windows.  On doing so, a set of five options panels appear as follows:

 

 

On clicking the Waveform tab the following panel appears:

 

 

 

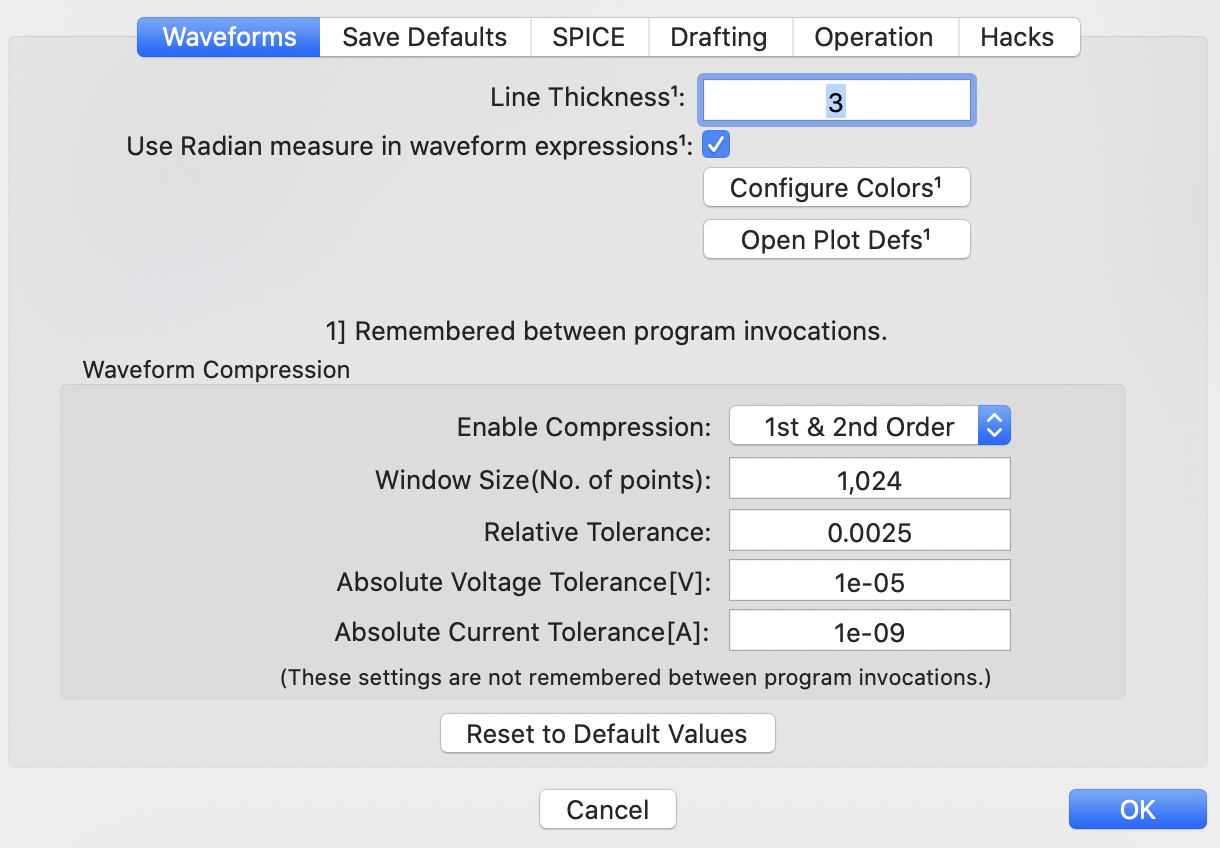
The thickness of each line can be selected.  Here a line thickness of 3 is selected.  This enables the lines to be clearly seen when printed. Further clicking on the Configure Colors button, leads to the following three-color setting pallets:

 

 

 

 

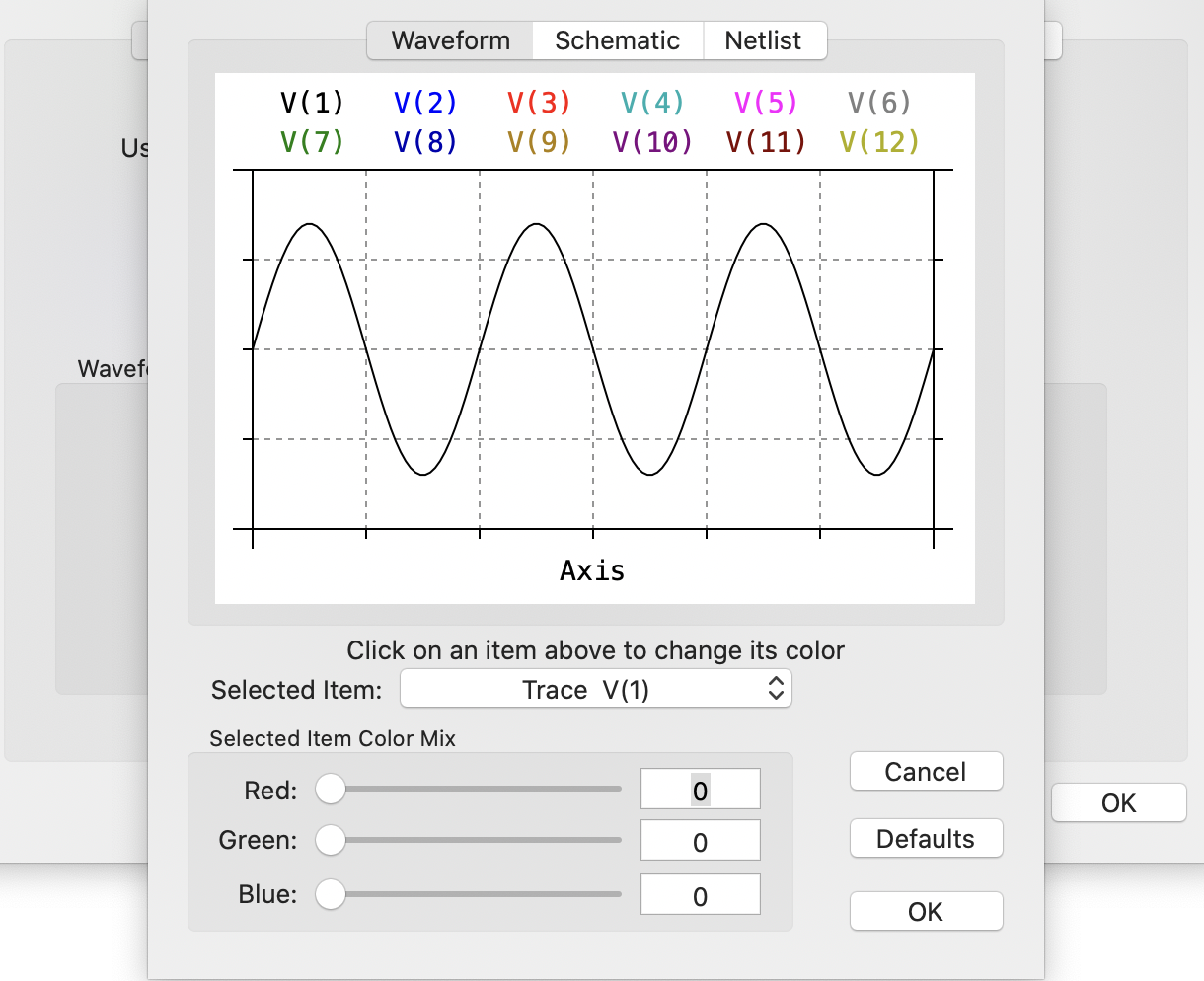
Here the colors can be easily controlled by clicking on the Selected Item button and setting the colour of each item. Generally, a white background, black labels and different colors for various traces seems to work best.

 

 

 

 

1.3.2 Spice Description Language (SDL)

 

The Spice Description Language (SDL) was first introduced by L. Nagel in 1972 [1] and has become an industry de-facto standard. Later versions of the Spice program, including LTSpice, allow alphanumeric node labeling to improve the readability of the SDL. The file that contains a circuit described using SDL is commonly referred to as a Spice input file or circuit netlist.  Each line is either a statement describing a single circuit element or a control line setting model parameter, measurement nodes, or analysis types. The first line in the Spice input deck must be a ``title’’ to identify the output generated by Spice; be careful with blank lines at the top of the file as this will force the title line to be misread. The last line in the Spice deck must be an ``.END ‘’ statement. The sequence of the lines between the title and .END statements are arbitrary.  Based on the authors' experience, the format shown in Fig. 1.2 is recommended for the Spice input file's layout.  Comments sprinkled throughout the file improve its readability, identify components of the design, and explain the rationale for the simulation.  They are designated by inserting an ``*’’ as the first character in this line.

 

Each statement is of the free-format type; that is, the words used in each statement can be separated by either arbitrary-sized spaces (limited, of course by the line length) or commas, or both. Lines longer than 80 characters (i.e., the screen width), can be continued on the next line by entering a + (plus sign) in the first column of the new line. The original version of Spice was all upper case, but LTSpice make no distinction between upper and lower case. In our future examples we will mix the case type for easy reading. A number can be represented as either an integer or floating point, using either decimal, scientific notation or engineering scale factors. The recognized scale factors are listed in Table 1.1. Not included in this table, but recognized by Spice, is the suffix MIL which is equivalent to 1/1000th of an inch. In addition, the dimensions or units of a given value can also be appended to any element value to clarify its context.  The allowed suffix types are listed in Table 1.2. One word of caution about attaching Farads to a capacitor value. Spice, unfortunately, uses the same letter (F) to denote a scale factor of 10^-15 (femto) -- see Table 1.1. One must therefore be careful not to confuse these two suffixes in a Spice input file.  Placing a single suffix F on the value of a capacitor indicates that the value of the capacitor is to be expressed in femto-farads not farads. Thus 1 F is 10^-15 farads while 1 with no suffix is one farad.

 

 

 

The Spice simulation process begins when we draw a clearly labeled circuit diagram with all nodes distinctly numbered with nonnegative integers between 0 - for the ground node - and 10,000 preceded with the letter n or N.  The ground node reference does not include an n or N before the zero value. All components are to be uniquely labeled; no two components should have the same name.  Figure 1.3(a) shows a linear network consisting of various resistors, capacitors and sources (both dependent and independent) with values indicated.  This is the same one that appeared in Fig. 1.1. In Fig. 1.3(b) each element is assigned a unique name in which the beginning letter (e.g., R, C, E, V) indicates the element type, e.g., R for resistor, D for diode, etc.  Table 1.3 lists such key letters available in Spice. For example: the 1-ohm resistor is assigned the name R₁, the load resistor of 10 ohm is R_load, the 2.65 mF capacitor is C₁, the voltage-controlled voltage source is E₁ and the input sinusoidal voltage source is v_i.  The ground node is labeled 0, and the remaining non-grounded nodes are assigned the numbers n1, n2, and n3.

 

The Spice input deck is made up of three major components: a detailed circuit description, analysis requests, and output requests.  We now outline the basic syntax of the various commands in these three Spice components.

 

Circuit Description

 

Each circuit element is described to Spice by an element statement which contains the element name, the circuit nodes to which it is connected, and its value. Spice knows about four general classes of network elements: passive elements, independent sources, dependent sources, and active devices (i.e., diodes and transistors).

 

The general Spice syntax for an element description is that the first letter indicates the element type, followed by an alphanumeric name limited to 7 characters which uniquely identifies that element. The information following the element type and name depends on the nature of the element. 

 

 

 

Passive Elements:         Fig. 1.4 depicts the Spice single-line descriptor statements for an arbitrary resistor, capacitor and inductor. The first field (or set of characters separated by blank spaces) of each statement describes its type and provides a unique name for each element. The next two fields indicate the alphanumeric label of the connecting nodes. Although these elements are bilateral, each element is assigned a positive and negative terminal. This convention assigns direction to the current flowing through each device as denoted in Fig. 1.4, but more importantly, it specifies the polarity of the initial conditions as associated with the energy storage devices. The fourth field is used to specify the value of the passive element. Resistance is in Ohms, capacitance in Farads and inductance in Henries. These values are usually positive but can also be assigned a negative value (in which case the elements are not passive). For either the capacitor or inductor, an initial (time-zero) voltage or current condition can be specified in its fifth field (See Fig. 1.4).

 

For the circuit in Fig. 1.3, the element statements for passive elements R₁, C₁ and R_load would appear in the Spice netlist:

 

 

 

For easy reading, we have attached the dimensions of each element on the end of each parameter value.

 

 

 

 

 

 

 

Independent Sources:            There are three types of independent sources that can be described to Spice: a DC source, a frequency-swept AC generator, and various types of time-varying signal generators. The independent signal associated with any one source can be either voltage or current. Fig. 1.5 gives a shortened summary of the description of these various sources with the kind of analysis that would be most appropriate for the source type.

 

With regards to the Spice description of each of these signal sources, the first field begins with the letter V or I, depending on whether it is a voltage or a current source, respectively, followed by a unique 7-character name. The next two fields describe the nodes to which the source is connected to the rest of the network. It is important to respect the order of the nodes because of the signal polarity associated with the source. For example, in the case of a voltage source, the first node is connected to the positive side and the second node to the negative side.  As far as the polarity (sign) of the current through a voltage source is concerned, the convention in Spice is as follows: Current flowing into the positive terminal of the source is taken as positive. In the case of a current source, a positive current is pulled from the positive node (n+) and returned to the negative node (n-).  The next field specifies the nature of the signal source, i.e. DC, AC or time varying. The remaining fields are then used to specify the characteristics of the signal waveform generated by the particular source.  The subsequent signal level parameters associated with the DC and AC sources should be obvious from the Spice descriptions listed in Fig. 1.5. The signal level of the DC source is specified by the field labeled value.  The peak amplitude and the phase (in degrees) of the AC source are simply specified in the fields labeled magnitude and phase_degrees, respectively. If the field labeled by phase_degrees is left blank, Spice will assume that the phase is zero.

 

In addition to DC and AC sources, one can also describe several different types of time-varying signal sources as listed in Fig. 1.5. Included in this list are element statements describing a sinusoidal signal (denoted by the SIN flag), a periodic pulse signal (PULSE) and an arbitrary waveform consisting of piece-wise linear segments (PWL).  Obviously, due to the time-varying nature of these signals, these sources can only be used in transient analysis studies. The syntax of these time-varying sources is more complex than that for the DC or AC sources described above, so to simplify matters, we list in Fig. 1.6, the corresponding waveform with the appropriate signal-determining parameters superimposed on each waveform. Although we express these waveforms in terms of voltage, it should be readily apparent that similar waveforms can be described for current sources.

 

For the circuit example of Fig. 1.3, the input sinusoidal voltage source v_I described by 10 sin (2p 60 t) would have the following Spice description:

 

Vi 1 0 SIN ( 0V 10V 60Hz  0 0 ).

 

In many cases, the delay time t_d and the damping factor damp are both zero, so we commonly shorten the above Spice statement to:

 

Vi 1 0 SIN ( 0V 10V 60Hz ).

This is acceptable to Spice.

 

Linear Dependent Sources:    Spice knows about four dependent sources:  voltage-controlled voltage source (VCVS), voltage-controlled current source (VCCS), current-controlled voltage source (CCVS) and current-controlled current source (CCCS).  These can be either linear or nonlinear, but here we are concerned only with the linear ones. Fig. 1.7 depicts all four sources with the relationship between their input and output variables made clear and also shows the statement used to describe the element to Spice. The name of each dependent source begins with a unique letter (i.e., E, G, H and F) followed by a unique 7-character name exactly like the passive elements described above.

 

Each dependent source is a two-port network with either the voltage or current at one port (terminals denoted as n+ and n--) controlled by the voltage or current at the other port (terminals denoted as nc+ and nc- ). For the voltage-controlled dependent source, the controlling voltage is derived directly from the network node voltages. A current-controlled source, however, must sense a current through a short circuit that is described to Spice using a zero-valued voltage source, i.e., Vname nc+ nc- 0. This means a current-controlled source requires two statements where a voltage-controlled source needs only one -- an aspect to keep in mind when working with current-controlled dependent sources.

 

The gain factor associated with the input and output variables is specified in the field labeled value and its dimensions will depend on the type of the dependent source.  For example, the voltage-controlled voltage source in the circuit of Fig. 1.3 can be described to Spice as follows:

 

E1  n3  0  n2  0  10.

 

Active Devices:                       The real computational strength of Spice lies in its ability to simulate the behavior of various types of active or electronic devices such as diodes, bipolar transistors, and field-effect transistors.  More recent versions of Spice have been extended to include gallium arsenide transistors and several other types of semiconductor devices.

 

Active devices are described to Spice in much the same manner as electrical elements: a statement indicating the device type and name followed by the nodes by which it is connected to the rest of the network. The subsequent fields refer to a specific model statement found on another line of the Spice netlist. The model then contains the parameters of the device and the nature of the device model, e.g., npn bipolar transistor. Most active device models are quite sophisticated and consist of many parameters, so this approach has the advantage that more than one device can reference the same model, simplifying data entry to the Spice input file. We defer detailed discussion on active devices until Chapter 3 on diode circuits.

 

 

 

Analysis Requests

 

Once a circuit is described to Spice via an input file, we must specify the analyses directive required for simulation.  We have three main choices:  DC operating-point, AC frequency response, and transient response. Table 1.4 shows their syntax plus that of the DC sweep command.  Notice that each of these commands begins with a dot ``. '' , which tells Spice that the line is a command line requesting action, not part of the circuit description.

 

The command requesting a DC operating point calculation is .OP and it includes finding all the DC node voltages and currents, and the power dissipation of all voltage sources (both dependent and independent). The .OP command automatically prints the calculation results in the output file. 

 

In general, to determine a circuit's DC transfer characteristic, we need to vary the level of some DC source.  We could run repeated. OP commands, but Spice provides a DC Sweep command (.DC) that performs this calculation automatically. The syntax of this command is: the name of the DC source to be varied ( source_name) beginning at the value marked by  start_value and increased or decreased in steps of  step_value until the value  stop_value is reached.  A second nested iteration loop can also be included.  This is very handy for creating 3-dimensional plots.  One can also vary the temperature of the circuit by replacing the name of the source in the field labeled  source_name by TEMP. 

 

With the AC frequency response command (.AC), Spice performs a linear small-signal frequency response analysis. It automatically calculates the DC operating point of the circuit, thereby establishing the small-signal equivalent circuit of all nonlinear elements.  The linear small-signal equivalent circuit is then analyzed at frequencies beginning at freq_start and ending at  freq_stop. Points in between are either spaced logarithmically by decade (DEC) or octave (OCT). The number of points in a given frequency interval is specified by points_per_decade or points_per_octave.  We can specify a linear frequency sweep (LIN) and the total number of points in it by total_points.  We usually use a linear frequency sweep when the bandwidth of interest is narrow, and a logarithmic sweep when the bandwidth is large. 

 

Finally, with the transient response command (.TRAN), Spice computes the network variables as a function of time over a specified time interval. The time interval begins at time t=0 and proceeds in linear steps of time_step seconds until time_stop seconds is reached.  Although all transient analysis must begin at t=0, we have the option of delaying the printing or plotting of the output results by specifying the no_print_time in the third field enclosed by the square brackets.  This is a convenient way of skipping over the transient response of a network and viewing only its steady-state response.  In order to have Spice avoid skipping over important waveform details within the time interval specified by time_step, the field designated by max_step_size should be chosen to be less than or equal to the time_step. For most, if not all examples of this text, we chose the max_step_size equal to the time_step.

 

Prior to the start of any transient analysis, Spice must determine the initial values of the circuit variables, usually from a DC analysis of the circuit. If the optional modifier: UIC (use initial conditions) parameter is specified on the .TRAN statement, then Spice will skip the DC bias calculation and instead use only the ``IC='' information supplied on each capacitor or inductor statement (see Fig. 1.4). All elements without an ``IC='' specification are assumed to have an initial condition of zero. LTSpice also provides other types of modifiers such as stop the simulation on reaching steady-state (steady).  Interested readers can refer to the LTSpice on-line User Manual for more information.

 

Initial conditions can also be set using an .IC command which clamps specific nodes of the circuit at the user-specified voltage levels during the DC bias calculation. This DC solution is then used as the initial conditions for the transient analysis.  The syntax of the .IC statement is listed under the .TRAN command in Table 1.4. Note that this command is not used with the UIC flag of the transient analysis command. 

 

Spice can perform many variations of the above-mentioned analysis, as mentioned previously. However, it is felt that at this time introducing these additional commands would only burden our readers with details that will not be used until later chapters of this text. Therefore, we shall defer discussion of these additional commands until a more convenient time.

 

 

 

 

Output Requests

 

Circuit simulation produces a lot of data, and it would be impractical to pass all of it on to the user. SDL includes commands to list out specific results in various formats, such as .PRINT and .PLOT. However, such features were never installed in LTSpice.  Rather, the data can only be displayed using the built-in waveform displayer. On execution of an LTSpice analysis, a window will appear with title: myproject.raw. By moving your mouse over any node on the circuit schematic, a probe symbol will appear; By click on a node with the probe symbol highlighted will result in a waveform appearing in the waveform display window. The waveform will be given a name that corresponds to the node name that LTSpice assigns to it.  Often, it is best to re-label the node using the Net Name tab with a name that has specific meaning, i.e., output, input, reference, etc..

 

LTSpice also allows for the display of component currents.  Drag the mouse over a component and a magnetic-field clamp-probe appears. By clicking on this, a current waveform appears in the waveform display window. If mixed variables are displayed at the same time, there will be a separate axis corresponding to each quantity, i.e., voltage and current. Some analysis directives (such as .OP) will allow a waveform to display a specific node voltage or component current, but will also save the entire analysis set of circuit variables in the log file. There are other analysis directives not yet mentioned that do this as well.  These will be introduced in later chapters.

 

Finally, the waveform viewer allows for mathematical operations to be performed on the circuit analysis variables.  Two or more circuit variables can be entered into an expression involving addition, subtraction, multiplication and /or other operations as described in Table 1.5.  Furthermore, one can incorporate various functions of a single circuit variable into these expressions. Table 1.6 provides a listing of the various operations available in LTSpice.   For instance, the absolute value of the voltage on node 1 would be written as abs(V(1)).  LTSpice performs a dimensional analysis on the result and will plot it along a corresponding vertical axis.

 

For complex data, the functions atan2(,), sgn(), u(), buf(), inv() uramp(), int(), floor(), ceil(), rand(), min(,), limit(,), if(,,), and table(...) are not available. The functions Re(x) and Im(x) are available for complex data and return a complex number with the real part equal to the real or imaginary part of the argument respectively and the imaginary part equal to zero. The functions Ph(x) and Mag(x) are also available for complex data and return a complex number with the real part equal to the phase angle or magnitude of the argument respectively and the imaginary part equal to zero. The function conj(x) is also available for complex data and returns the complex conjugate of x.

 

Several physical constants are internally defined in LTSpice and can be used in any mathematical expression. These can be found listed in Table 1.7.

 

The waveform viewer can integrate a trace to obtain the average and RMS value over some region defined by the user. In a rather indirect manner, these values are obtained by zooming in on the waveform over the region of interest, move the cursor over the label of the trace, hold down the control key and click the left mouse button.   A window will appear that provides the average and RMS value of the signal over the start and stop time interval as follows:

 

 

 

An FFT of some of the circuit variable waveforms can also be displayed. This is a plot of the spectral coefficients in units of dB referenced to 1 V rms versus frequency. Place the mouse in the waveform view window. Right click and navigate the mouse over the View tab then the FFT tab; right or left click the mouse  and the FFT selection window will appear.  Select the appropriate circuit variable (only those highlighted can be used) and a new window will appear with the FFT result as shown below:

 

 

 

A Simple Example

 

For the simple circuit of Fig. 1.3 (repeated below) let us create a Spice input file using SDL that would be used to compute the transient response of this circuit for 3 periods of a 10 V, 60 Hz sinusoidal input signal. The Spice input file for this circuit would appear:

 

 

 

The first line begins with the title:  ``Transient Response Of A Linear Network,'' followed by a circuit description, analysis request and several output request statements. The final statement is an .END statement. Comments are sprinkled throughout this file to improve its readability. The transient analysis statement,

.TRAN 1ms 50ms 0ms 1ms,

 

is a request to compute the transient behavior of this circuit over a 50 ms interval using a 1 ms time step.  The results of the analysis are to be stored in resident memory beginning at time t=0 and will later be available for printing or plotting. The last field specifies that the maximum step size is to be limited to 1. ms, the same value as the time step. To simulate this circuit, copy the SDL file and drop it into the SPICE Netlist window that was first opened (see Fig. 1.1).  Move the mouse over the hammer icon  and left click. A simulation window will appear, just click OK.  The simulation process will begin. 

 

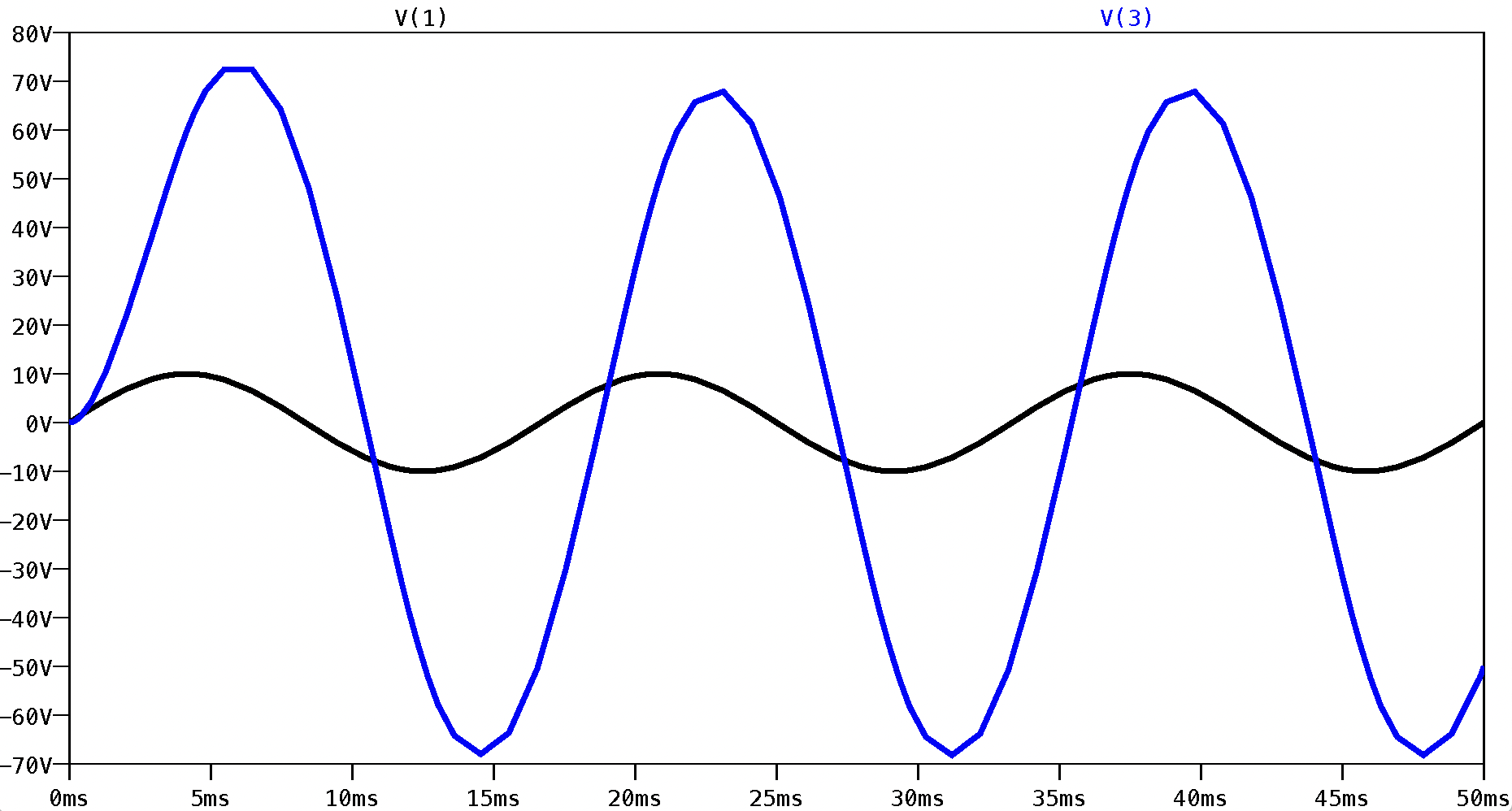
On completion, the waveform viewer window will appear.  Move the mouse into this window and place it over the variable selection icon at the top  and click the left mouse button.  Select the input and output voltage variables, V(1) and V(3).  The following plot appears in the display window:

 

 

1.3.1 Schematic Circuit Entry

 

A preferred method to simulate a circuit with LTSpice is to enter the schematic circuit into LTSpice using its drawing capabilities. LTSpice will then translate the circuit schematic into an SDL text file (myproject.net) and then, when instructed, run the circuit simulation engine. To enter the schematic, the drawing capabilities of LTSpice is used to place components, select their values and run wires between them. Analysis directives such as those seen listed in Table. 1.4 are made by typing them directly onto the circuit schematic page.

 

To begin a drawing, place the mouse icon inside the myproject.asc window and right click.  A pull-down menu that the user has seen before in Fig. 1.1 appears.  This time slide the mouse icon over the Draft tab. This results in a secondary pull-down menu that appears as follows:

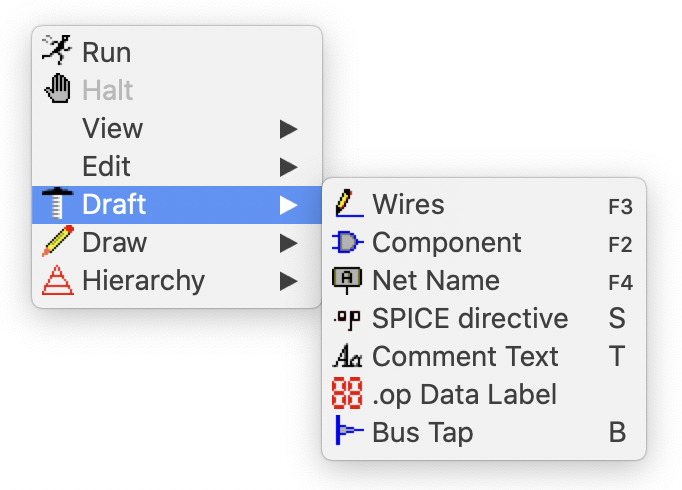
This menu lists all the primitives used to create a circuit schematic. The Component tab brings up a large list of possible components to select and incorporate into one’s design.  This includes basic passive elements like resistors and capacitors, active elements such as BJT and MOS transistors, as well as a large database of commercial components from Analog Devices such as op-amps and voltage regulators. It is the latter reason that motivates Analog Devices Inc. to provide such a powerful simulation tool for free.  The Wires tab sets the interconnection between two or more components.  The tab labelled Net Name provides the GND node that must be included with all circuit schematics.  Further, this tab provides a means to give unique names to circuit nodes. This is useful when displaying node voltages with a known name rather than some arbitrary number that LTSpice generates, as well as a secondary means to interconnect two or more components together without adding a wire. The Analysis and Comment tabs provides a means to enter text that appears on the schematic. Any text can be toggled between a SPICE directive or a comment statement. A comment has no effect on a simulation. A SPICE directive, however, determines the type of analysis that will be performed when the simulation begins.  Only one SPICE directive is allowed at any one time. While there may be numerous SPICE directives associated with any one circuit schematic, only one can be active at a time.  The others must be toggled to a comment statement.  The other remaining tabs are for the advanced user and will not be discussed here.  As an example, in the upper left-hand corner of Fig. 1.1 is a schematic circuit of an RC circuit with independent and voltage-dependent voltage sources.  This was drawn using the steps described above.  The specific details about the components that the user has to enter will be described in the next subsection where the Spice Description Language (SDL) will be introduced.  Generally, during schematic entry this information is entered through a table by right-clicking on a component. Click on this link to see a short video that goes through the steps to capture a circuit schematic in LTSpice.

 

 

1.4 Examples

 

The first example involves calculating the DC node voltages of a linear network, the second explores the transient behavior of a three-stage linear amplifier subject to a sine-wave input, the third illustrates how circuit initial conditions are established during a transient analysis, and the last example computes the frequency behavior of a linear amplifier.

 

 

 

 

 

1.4.1 Example 1: DC Node Voltages Of A Linear Network

 

Our first circuit example is shown in Fig.  1.8(a) which displays a rather complicated network of resistors and sources. Sources V_S1, V_S2, and I_S1, are independent DC sources whose values are given on the circuit schematic. The remaining two sources, v_c1 and i_c1, are dependent sources where v_c1 is a current-controlled voltage source (CCVS) and i_c1 is a voltage-controlled current source (VCCS).  In the case of v_c1, the voltage generated by this source is proportional to the current that flows through the 1-ohm resistor, designated by i₁. On the other hand, the current generated by i_c1 is proportional to the voltage appearing across the 3 ohm resistor.

 

The first step in preparing the circuit schematic of Fig. 1.8(a) for a LTSpice simulation is to identify each element of the circuit by assigning it a unique name, and then, label each node of the circuit with some non-negative integer preceded by the letter n. It is also necessary to label the ground node of the circuit as node 0.  Preceding each node number by n only matters with an operating point analysis. There seems to be a programming glitch when writing the operating point analysis results into the log file.   The results of this labeling process are shown in the circuit diagram displayed in Fig.  1.8(b).  Further, due to the presence of the CCVS, a zero-valued voltage source must be placed in series with the 1-ohm resistor (R₁) in order to sense the current through it.  Thus, we have added a zero-valued voltage source V3 in series with R₁.  Recall from Fig 1.7 that this is a necessary requirement for describing current-controlled sources to Spice.

 

Our next step is to provide the Spice directive command.  Here the command .OP has been added to the schematic. This command directs LTSpice to compute the DC operating point of the circuit.  A quick review of the LTSpice generated SDL netlist seen in Fig. 1.9 ensures the correct SPICE directive is included and no funny node labeling appears.  We do note that the Spice directive .backanno appears that was not included with the schematic capture process.  This command was automatically added by LTSpice.  This command directs LTSpice to include information in the waveform data file to keep track of different port currents. 

 

On execution, the results of the operating point analysis are found in the Spice error log file (*.log) and is shown listed in Fig. 1.10.  The data is listed in two parts.  The first part contains a listing of all the node voltages, as per the naming assignment made in Fig. 1.8(b). Following this are the resistor currents and the currents associated with the independent and dependent sources.

 

 

 

 

 

 

 

 

1.4.2 Example 2: Transient Response of A 3-Stage Linear Amplifier

 

Our next example is shown in Fig.  1.11(a) which consists of a three-stage linear amplifier fed by a signal source having a source resistance of 100 k-ohm. Hand analysis reveals this circuit has an overall voltage gain, A_v = v_L /v_s, of 743.6 V/V, a current gain, A_i=i_o / i_i, of 8.18 x 10⁶ A/A, and a power gain, A_p=A_v x A_i, of 98.3 dB. Here we shall compute the same gains by using the transient analysis capability of Spice and the graphical post-processing features of LTSpice and compare the results with those found by hand.

 

We begin by capturing the circuit diagram shown in Fig.  1.11(a) using LTSpice.  The result is shown in Fig. 1.11(b).   The input and output nodes of the amplifier have been labelled IN and OUT, and the source node as S. The remaining nodes have been given a numerical number assignment; no need to label with a preceding n letter, as this is only necessary with an .OP type analysis.   The ground node has been labeled as 0.  The input generator is a 1-volt time-varying sinusoidal voltage source of 1 Hz frequency with zero voltage offset.  Using the .TRAN Spice directive the time response of the circuit from t=0 to t=5 s in 10 ms time steps will be computed. The LTSpice input file is shown in Fig. 1.12.  This file confirms our labeling and requests; no funny characters have managed to get into the file.

 

On completion of LTSpice, we use waveform displayer to view the results. In Fig. 1.13(a) we plot both the input voltage (v(s)) and output voltage (v(out)) as a function of time.  As the two signals are in phase, the voltage gain V(out)/V(in) is simply the ratio of the peak values. The peak value of the waveform is found by placing the mouse over the peak point on the waveform and reading off the x-y value provided.  Here we find the peak value are 743.19 V for the output signal and 1 V for the source signal. Thus, the voltage gain is 743.19 / 1 = 743.19 V/V.  This is good agreement with the hand analysis.    One can also ask the waveform view to plot the voltage ratio v(out)/v(s) and extract the peak value from this.  The results are the same, but possibly more accurate.

 

Similarly, the waveforms of the input current (i_i=i(R_i1)) and the load current (i_o=i(R_l)) are shown in Fig.  1.13(b).  The resulting current gain provided by this network is then calculated to be 8.18 MA/A.

 

As a final calculation, the waveform viewer was used to compute and display the instantaneous power delivered to the amplifier stage (v(in) x i(R_i1)) and to its load (v(out)xi(R_l)).  These waveforms are shown in Fig. 1.13(c).  The power gain is then found to be 6.69 GW/W or 98.3 dB. This also agrees with the hand calculation.

 

 

1.4.3 Example 3: Setting Circuit Initial Conditions During A Transient Analysis

 

There are three ways to set the initial conditions of a circuit at the start of a transient analysis. We demonstrate these on the simple RC circuit in Fig. 1.14(a). Drawing the circuit diagram with LTSpice results in the circuit schematic shown in Fig. 14(b).  Here the output node is label as OUT and all other nodes are labeled with a unique number.  As we plan to perform an operating point analysis, and want to look into the log file for the node voltages, the numerically labelled nodes are preceded with the letter n.  In the first case, the node voltages corresponding to the DC operating point of the circuit are calculated.  These node voltages will act as the initial conditions for the reactive elements of the circuit. The LTSpice input file resulting from this circuit is shown in Fig. 1.15. Setting the Spice directive with .OP command, one finds the DC operating point solution as follows:

 

Following this, a transient analysis of the RC circuit was performed over a 10 ms interval using a 500 us step interval using the following Spice directive:

 

TRAN 500us 10ms 0ms 500us

 

The results are shown in Fig. 1.16.  The top graph displays the voltage appearing across capacitor C₁, the middle graph displays the voltage appearing across capacitor C₂, and the bottom graph displays the voltage appearing at the output. As is clearly evident in all three cases, no change in the output voltage is taking place. This suggests that the initial conditions found by LTSpice were also the final time values.  Moreover, we see that these voltages are identical to the values found from the operating point analysis.

 

 

 

 

Next, let us consider setting the initial voltage across capacitor C₁ at +1 V and observe the effect that it has on the circuit operation. To do this, we must modify the element statement for C₁. One way to do this is to modify the netlist file (*.net) directly using the statement

 

C1 n1 0 1uF IC=+1V

 

or, one can make use of the attribute editor in the LTSpice command window by moving the mouse onto C₁ while holding down the CTRL key and right clicking the mouse.  This will bring up a new window. On the line corresponding to SpiceLine2, add the term IC=+1V.  To make this visible on the schematic diagram, left click on VIS column corresponding to this row and an X will appear.  Leave this window by clicking on okay; one will now see the capacitor C₁ updated with the initial condition IC=+1V. A view of the element statement for C1 in the netlist file will reveal exactly the statement above.

 

Next, alter the .TRAN statement using the modifier “UIC” according to

 

.TRAN 500us 10ms 0ms 500us UIC.

 

and execute. The results of this analysis are shown in Fig. 1.19.  Unlike the previous case, the voltages in the circuit are now changing with time.  At time t=0, we see that the voltage across capacitor C₁ is +1 V, as expected.  The voltage across C₂ at this time is 0 V by default (since it was not specified in the Spice netlist), and as a result, the output voltage is initially zero. As time progresses, we see that these three voltages converge to values identical to those found in the previous case (i.e. 3.33 V, 3.33 V and 1.667 V, respectively).

 

Another way of setting the initial conditions is with the .IC command line. This method is essentially a combination of the two previous methods.  The specific node voltages can be explicitly set, and the remaining nodes will take on values that result from the DC operating point analysis (with the initial value of appropriate nodes taken into account) instead of defaulting to zero.

 

For example, let us set the voltage at node 1 by using the following .IC command line:

 

.IC V(n1)=+1V

 

Add this statement directly on the schematic alongside the other Spice directives in the command window. We change the element statement for C₁ back to its original form,

 

C1  n1  0  1uF

 

and remove the UIC flag on the .TRAN statement to read as follows

 

.TRAN 500us 10ms 0ms 500us.

 

The results of this analysis are shown in Fig. 1.18.  Here we see that at time t=0 the voltage at node 1 begins at +1 V as specified.  In contrast to the previous case, the voltage at the second node does not begin at 0 V but instead begins with a value of 2.4 V. Likewise, the output voltage is no longer zero but begins at a voltage level of 1.2 V. The final values settle to the same values found previously in the other two cases. The moral of this example is to be extremely careful with the use of initial conditions and how they are used by LTSpice.

 

 

 

 

 

 

 

1.4.4 Example 4: Frequency Response of A Linear Amplifier

 

The final example of this chapter demonstrates how LTSpice is used to compute the small-signal frequency response behavior of a linear amplifier.  Figure 1.19 shows the small-signal equivalent circuit of a one-stage amplifier as captured by LTSpice.  Figure 1.20 list the corresponding SDL file translated from the circuit schematic.  While the input to the circuit is a sinusoidal signal, its AC attributes have been set to 1 V with 0 degrees. The AC spice directive will vary the frequency of the circuit between 1 Hz and 100 MHz logarithmically with 5 points-per-decade, as is indicated by the .AC analysis command. By selecting a 1 V input level, the output voltage level will also correspond to the voltage transfer function V_o/V_s since V_s=1.

 

The frequency response behavior of this amplifier was computed by LTSpice and the magnitude and phase of the output voltage V_o is seen plotted in Fig. 1.21(a).  There are two curves: one for magnitude and one for phase.  They both share the same horizontal axis (frequency) but have different vertical axis.  The vertical axis on the left is for the magnitude response of the amplifier and is expressed in dBs.  This is achieved by right-clicking on the left-hand side of the plot window alongside the vertical axis, resulting in a menu box with the axis range and the graph representation. The range was automatically set, and the graph representation was selected as a Bode Plot with the y-axis expressed in units of Decibel, as can be seen in Fig. 1.21(b).  One can also select a linear or logarithmic scale.  The user should explore the resulting graphs for themselves.   A similar selection box for the phase can be retrieved by right-clicking on the right-hand side to obtain the selection box shown in Fig. 1.21(c).  Here the Phase expressed in degrees or Group Delay (expressed in seconds) can be selected. As a rough estimate of the 3-dB bandwidth of this amplifier, we see from this graph that it ranges somewhere around 150 kHz.  A better estimate of the 3-dB bandwidth is obtained using the cursor facility of waveform viewer. This is done by moving the mouse to the trace label at the top of the screen and double-clicking the left mouse button. Two crosshair cursors appear, together with a dialog box, as illustrated in Fig. 1.21(d). Each cursor can be moved to different positions along the trace. The dialog box indicates the x-y co-ordinate position of each cursor, as well as their difference.  So, for the case here, one cursor was placed at the low end of the frequency axis to estimate the DC gain of the amplifier, and the other was positioned at higher frequencies so that their magnitude difference was 3 dB.  Hence, the 3-dB frequency was found to be 158.7 kHz.

 

This now concludes the Introduction to LTSpice.  Future chapters will explore different electronic circuit elements and how to simulate them with LTSpice.

 

1.5 Chapter Summary

 

·      Circuits are designed by people not computers; Spice or LTSpice can only validate the operation of human-designed circuits, as it does not design them.

 

·      Spice is an acronym for Simulation Program with Integrated Circuit Emphasis. It was originally developed for large main-frame computers in 1972.

 

·      LTSpice was originally written by the Linear Technology Corporation as part of its marketing strategy.  Linear Technology Corporation is now part of Analog Devices Inc.

 

·      LTSpice can run on Windows or OS X operating systems.  The interface is slightly different but fundamentally do the same operations.

 

·      LTSpice is a general-purpose circuit simulator capable of performing three main types of analysis---nonlinear DC, nonlinear transient, and linear small-signal AC circuit analysis.

 

·      SDL is an acronym for Spice Description Language; This language was created by Larry Nagel in 1972 for PhD. Dissertation at the University of California.

 

·      LTSpice operates on text files that conform with SDL; this file is called a circuit netlist.

 

·      A LTSpice circuit netlist is organized into two main parts:  circuit description and analysis request. 

 

·       The first line in an LTSpice netlist must be a title statement and the last line must be an. end statement.

 

·       A circuit is described to Spice by a sequence of element statements describing how each element is connected to the rest of the circuit and specifying its value. 

 

·       Each element type has a unique first-letter representation, e.g., R for resistor, C for capacitor.

 

·       LTSpice can perform other analysis as special cases of the three main analysis types;  One example is the DC Sweep command used to compute DC transfer characteristics. 

 

·       The results of circuit simulation are placed in an output file in either tabular or graphical form. 

 

·       LTSpice is equipped with a waveform viewer which allows for interactive graphical display of the simulation results. 

 

·       The waveform viewer can perform many powerful mathematical functions on any network variable created during circuit simulation. 

 

1.6       LTSpice Tips

 

·      The DC operating point of a circuit is found using the Spice directive

.OP

 

·      A DC transfer curve can be created using the following Spice directive:

.DC source_name start_value stop_value step-value

 

·      A small-signal AC analysis is performed using the following Spice directive:

.AC {LIN,OCT,DEC} points frequency_start frequency_stop

 

·      A small-signal transfer function analysis is performed using the following Spice directive:

.TF output_port input_source_name

 

·      A transient analysis is performed using the following Spice directive with initial condition:

.TRAN time_step time-stop no_print_time max_step_size

.IC V(node_1)=value V(node_2)=value ….

 

·       LTSpice is equipped with a waveform viewer which allows for interactive graphical display of the simulation results.  This waveform viewer is extremely versatile, as it has many built-in functions.

 

·      The mathematical operation performed using the waveform viewer is divided into multi-variable mathematical operations and single-variable operations; don’t confuse the two.

 

·      The waveform viewer has various physical constants stored in its internal memory.

 

·      LTSpice has many undocumented mathematical operations; these can be found using the vast set of resources found on the internet.  Often, I find these by reading the various user blogs.

 

1.7       Bibliography

 

L. W. Nagel, "SPICE2: A Computer Program to Simulate Semiconductor Circuits," PhD dissertation, Univ of California, Berkeley, CA, May 9 1975 and available as Memorandum No ERL-M520, Electronics Research Laboratory, College of Engineering, University of California, Berkeley, CA.

 

A. Vladimirescu, K. Zhang, A. R. Newton, D. O. Pederson, and A. Sangiovanni-Vincentelli, ``SPICE Version 2G6 User's Guide,'' Dept. of Electrical Engineering and Computer Sciences, University of California, Berkeley, CA, 1981.

 

Staff, LTSpice On-Line Users' Manual, Analog Devices Inc.

 

1.8   Problems

 

1.1.         For each of the circuits shown in Fig. P1.1 compute the corresponding node voltages using Spice.

 

1.2.         For each of the circuits shown in Fig. P1.2 compute the corresponding node voltages and branch currents indicated using Spice.

 

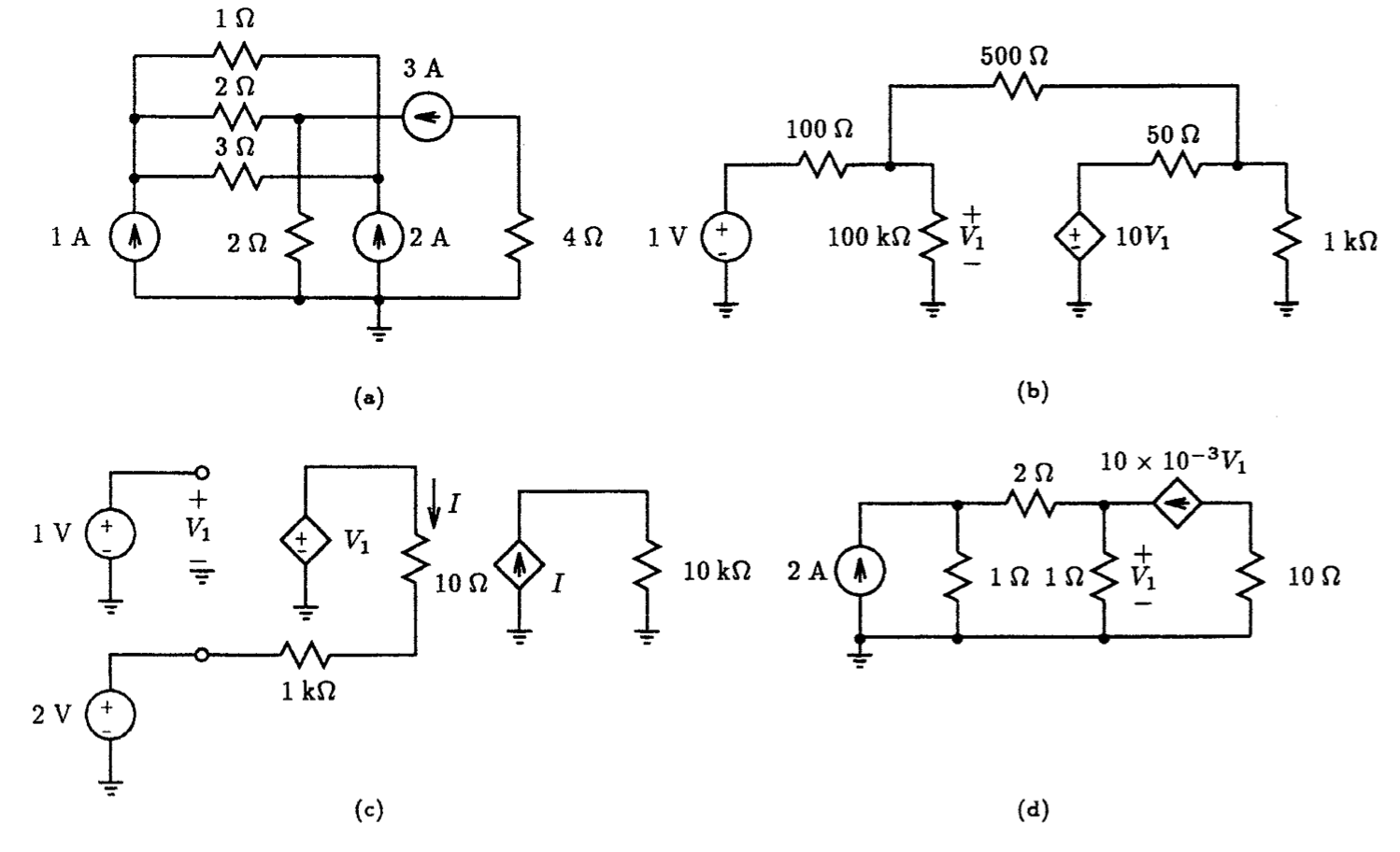
Fig. P1.1

 

Fig. P1.2

 

 

1.3.         Using the simple circuit arrangement shown in Fig. P1.3, generate a voltage waveform across the 1-ohm resistor having the following described form:

 

(i)          

 

(ii)          

 

(iii)        

 

(iv)         

 

 

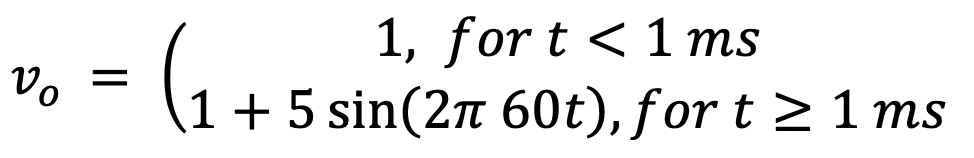
Verify your results using LTSpice by plotting the voltage waveform that appears across the 1-ohm resistor for at least 6 cycles of its waveform. Use a time step that samples at least 20 points on one cycle of the waveform.

Fig. P1.3

           

1.4.         Using the simple circuit arrangement shown in Fig. P1.3, generate a voltage waveform across the 1-ohm resistor having the following described form:

 

(i)             10 V peak-to-peak symmetrical square-wave at a frequency of 1 kHz. Let the rise and fall times be 0.1% of the total period of the waveform.

(ii)            8 V peak-to-peak asymmetrical square-wave at a frequency of 100 kHz having a DC offset of 2 V. Assign the rise and fall times of this waveform to be 0.1% of the total period of this waveform.

(iii)          10 V peak-to-peak asymmetrical square-wave at a frequency of 5 kHz having a DC offset of 2 V. Let the rise and fall times be 0.1% of the total period of the waveform.

 

Verify your results using LTSpice by plotting the voltage waveform that appears across the 1-ohm resistor for at least 6 cycles of its waveform. Use a time step that samples at least 20 points on one cycle of the waveform.

 

 

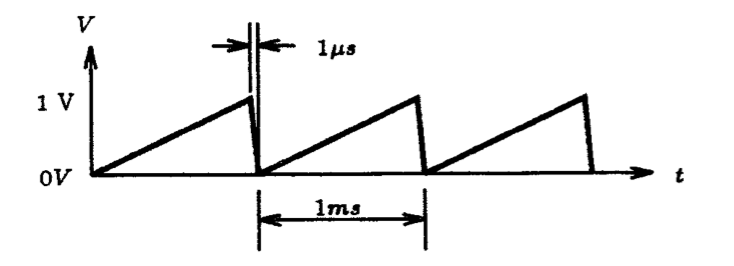
Fig.P1.6         

 

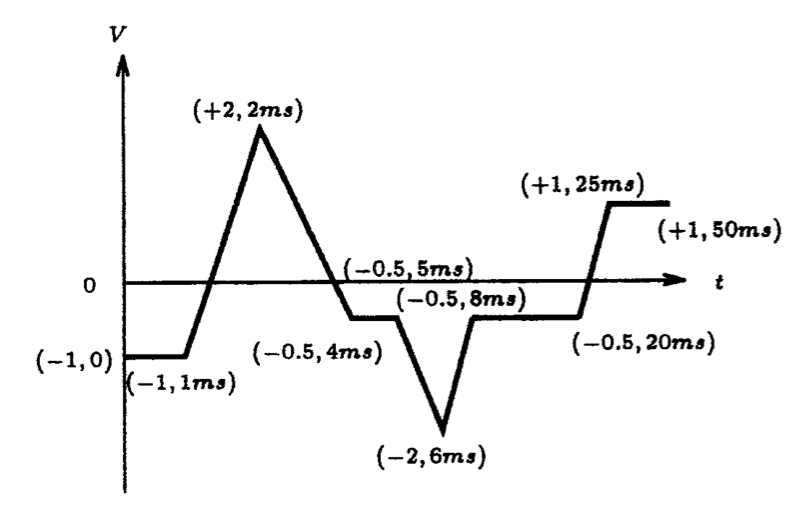
Fig. P1.7

 

 

1.5.         Replace the voltage source seen in Fig. P1.3 by a current source. Generate a current into the 1-ohm resistor using the PULSE source statement of LTSpice such that it has a triangular shape with an amplitude of 2 mA and a period of 2 ms. The average value of the waveform is zero. Plot this current for at least 6 cycles of its waveform using 10 points per period.

 

1.6.         Using the PULSE source statement of LTSpice, together with the circuit setup shown in Fig. P1.3, generate the saw-tooth voltage waveform shown in Fig. P1.6. Verify your results by plotting the voltage across the 1-ohm resistor for at least 6 cycles of its waveform.

 

1.7.         Using the PWL source statement of LTSpice, together with the circuit setup shown in Fig. P1.3, generate the voltage waveform shown in Fig. P1.7. Verify your results by plotting the voltage across the 1-ohm resistor for the full duration of this waveform. What voltage appears across the 1-ohm resistor if the simulation time extends beyond 50 ms?

 

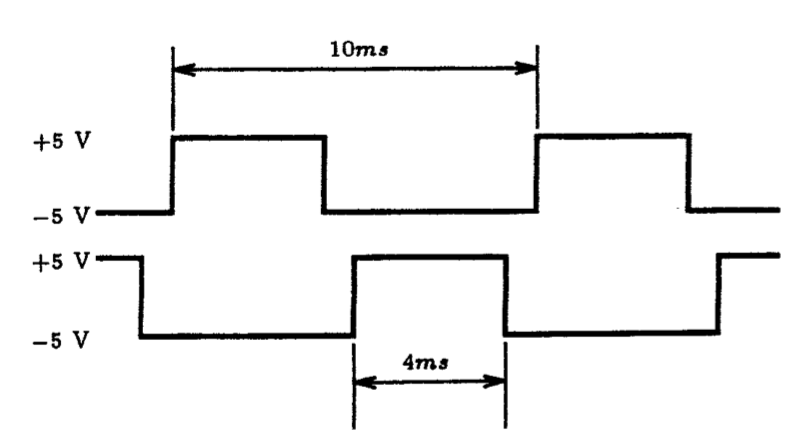
Fig. P1.8

 

1.8.         Using two voltage sources with appropriate loads, generate two signals that are non-overlapping complementary square-waves, such as those shown in Fig. P1.8.  Verify your results by plotting the voltage across each load resistor for at least 10 cycles of each waveform.

 

1.9.         Using the simple circuit arrangement shown in Fig. P1.3, generate a 0 to 1 V step signal across the 1-ohm resistor having a rise-time of no more than 1 us.  Verify your results using LTSpice by plotting the voltage waveform that appears across the 1-ohm resistor for at least 1 ms using a 50 us time step.

 

1.10.      For the first-order RC circuit shown in Fig. P1.10, simulate the behavior of this circuit with Spice subject to a 0 to 1 V step input having a rise time of no more than 10 ns.  Plot the voltage waveform that appears across the 1 k-ohm resistor and the 1 uF capacitor. Verify that the voltage across the capacitor changes by 63% of its final value in a time of one time constant.

 

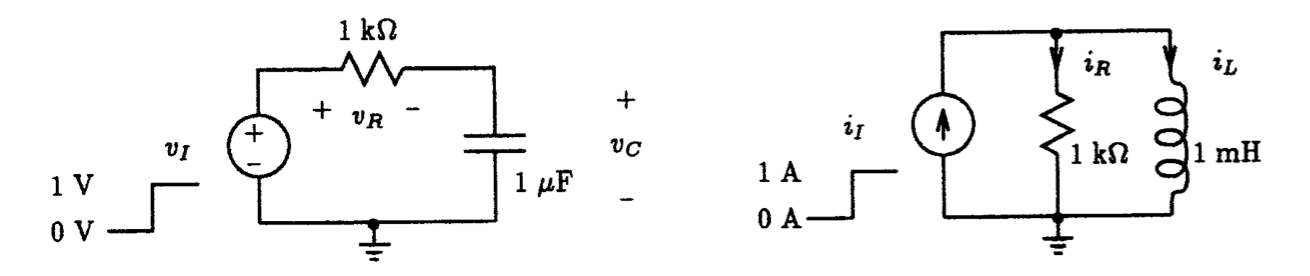
          Fig. P1.10                                                                                                                                                                                                        Fig. P1.11

 

1.11.      For the first order RL circuit shown in Fig. P1.11, simulate the behavior of this circuit with Spice subject to a 0 to 1 A step input having a rise time of no more than 10 ns.  Plot the current that flows in both the 1 k-ohm resistor and the 1 mH inductor. Verify that the current that flows in the inductor changes by 63% of its initial value in one time constant

 

1.12.      Repeat Problem P1.10 with the 1 uF capacitor initially charged to 0.5 V.

 

1.13.      Repeat Problem P1.11 with the 1 mH inductor initially conducting a current of 2 A.

 

1.14.      For the first-order RC circuit shown in Fig. P1.10 subject to a 1 V peak sine-wave input signal of 1 kHz frequency, simulate the behavior of this circuit with LTSpice.  Plot the voltage waveform that appears across the 1 uF capacitor for at least 6 cycles of the input signal. Use a time step that acquires at least 20 points per period.

 

1.15.      Repeat Problem P1.14 with a 1 V peak symmetrical square-wave input of 10 kHz frequency. How would you describe the voltage waveform that appears across the capacitor?

 

1.16.      For the first order RL circuit shown in Fig. P1.11 subject to a 1 A peak-to-peak triangular input signal of 1 kHz frequency, simulate the behavior of this circuit with Spice.  Plot the current waveform that flows through the 1 k-ohm resistor for at least 6 cycles of the input signal. Use a time step that acquires at least 20 points per period. How would you describe this current waveform?

 

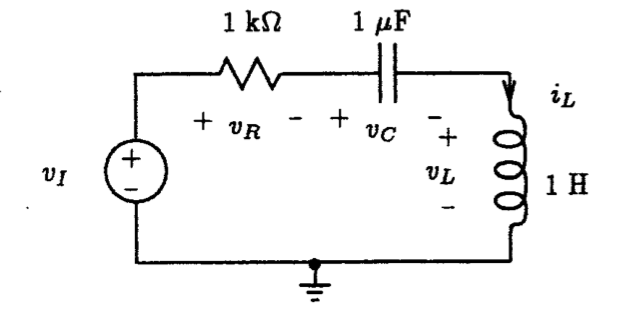
Fig. P1.17

 

1.17.      For the second order RLC circuit shown in Fig. P1.17 subject to a 1 V step input, simulate the transient behavior of the circuit and plot the voltage waveform that appears across each element for about 40 ms. Use a time step of no more than 100 us.

 

1.18.      Repeat Problem 1.17 with value of the resistor decreased by a factor of 10. How do the waveforms compare with that in Problem 1.17.

 

1.19.      Repeat Problem 1.17 with value of the resistor decreased by a factor of 100. How do the waveforms compare with that in Problem 1.17.

 

1.20.      Compute the frequency response behavior of the RC circuit shown in Fig. P1.10 using LTSpice for a 1 V AC input signal. Plot both the magnitude and phase behavior of the voltage across the resistor and the voltage across the capacitor over a frequency range of 0.1 Hz to 10 MHz. Use 20 points-per-decade in your plot.

 

1.21.      Compute the frequency response behavior of the RL circuit shown in Fig. P1.11 using LTSpice for a 1 A, AC input signal. Plot both the magnitude and phase behavior of the current through the resistor and inductor over a frequency range of 1 mHz to 1 MHz. Use 10 points-per-decade in your plot.

 

1.22.      Compute the frequency response behavior of the RLC circuit shown in Fig. P1.17 using LTSpice for a 1 V AC input signal. Plot both the magnitude and phase behavior of the voltage across the resistor, inductor and capacitor over the frequency range of 1 Hz to 1 kHz.  Use 10 points-per-octave in your plot.

 

1.23.      Compute the frequency response behavior of the RLC circuit shown in Fig. P1.17 with R having values of 10, 100 and 1 k-ohm.  Plot the magnitude and phase response of each case and compare them. Select an appropriate frequency range and number of points that best illustrate your results.